Kódování

Created by Bc. Lukáš Vokurka, DiS

Topic of the project: Coding in 5G Mobile Networks

Mobilní síť 5G

Pátá generace mobilních sítí je telekomunikační standard, který navazuje na 4G LTE. Základní požadavky na systém 5G byly definovány v IMT - 2020. Pravda je taková, že implementace 5G je velmi náročný proces, jak ekonomicky, tak i časově. Musí se tedy počítat s tím, že systém je implementován postupnými kroky, jak budou uvolňovány další specifikace standardu 5G tzv. Release, které definuje 3GPP, což je projekt, na kterém spolupracují skupiny telekomunikačních sdružení s cílem vyvinout celosvětově platné specifikace pro mobilní systémy. Proces standardizace pro 5G je dokončen formou příslušné specifikace jako Release 15. Aktuálně probíhá implementace specifikace Release 18. Nová architektura systému 5G se nazývá SBA (Service - Based Architecture).

Nové služby 5G jsou dle 3GPP a ITU definovány následujícím způsobem:

• eMBB (Enhanced Mobile BroadBand) – vylepšení mobilní širokopásmové připojení,

• mMTC (Massive Machine – Type Communication) – masivní komunikace mezi zařízeními,

• uRLLC (Ultra-Reliable Low Latency Communication) – vysoce spolehlivá služba s nízkou latencí.

Režimy 5G NR (New Radio)

V praxi mobilní operátoři využívají DSS (Dynamic Spectrum Sharing), což označuje technologii, která umožňuje používat mobilní bezdrátové technologie 4G LTE a 5G NR ve stejném frekvenčním pásmu a zároveň dynamicky přidělovat šířku pásma na základě požadavků koncových uživatelů.

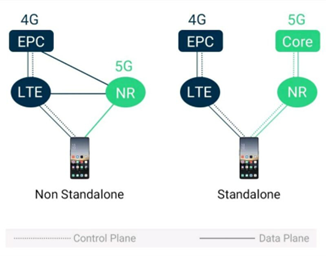
• NSA (Non - Stand Alone)

Tato architektura je založena na existujících sítích 4G LTE a využívá infrastrukturu pro řízení sítě a signalizaci (Control Plane) přes jádro EPC (Evolved Packet Core), zatímco 5G se používá pro přenos uživatelských dat (Data Plane). Znamená to, že koncová zařízení musejí být schopna podporovat, jak 4G, tak i 5G technologie. NSA umožňuje rychlejší nasazení 5G sítí.

• SA (Stand Alone)

Tato architektura je plně samostatná a nezávislá na existujících sítích 4G LTE. V této architektuře jsou všechny prvky sítě 5G postaveny do základů a 5G sítě řídí a signalizují pomocí samostatného jádra sítě 5G – Core.

Kanálové kódování

Kanálové kódování zahrnuje implementaci ECCs (Error Correction Codes)/FEC (Forward Error Correction) na fyzické vrstvě telekomunikačního systému. Je to tedy technika, užívaná ke kontrole chyb při přenosu dat skrze komunikační kanál, v nichž dochází k šumu, a tedy i ke ztrátě informací. Hlavní myšlenkou je, že odesílatel informaci kóduje nadbytečně (redundance) pomocí samoopravného kódu, kdy nadbytečnou informací umožní příjemci detekovat a limitovat množství chyb, které se mohou objevit, kdykoliv a kdekoliv během přenosu informace a často také opravit tyto chyby bez nutnosti znovu odeslání zprávy.

Kanálové kódování v 5G NR

Ve specifikaci 3GPP Release 15 byla zavedena nová schémata pro kanálové kódování fyzické vrstvy, konkrétně polární kódy a LDPC (Low-Density Parity-Check), které mají nahradit konvoluční a turbo kódy používané ve 4G LTE. V 5G NR se pro datový kanál (Data Plane) používájí LDPC a pro řídící kanál (Control Plane) polární kódy.

LDPC

Jak už bylo zmíněno, tak LDPC kódy byly specifikovány ve 3GPP Release 15 a používají se pro fyzické kanály PDSCH (Physical Downlink Shared Channel) a PUSCH (Physical Uplink Shared Channel), které přenášejí uživatelská data (Data Plane). Chyby kanálu opravuje zachováním paritních bitů pro vybrané datové bity, kdy většina datových bitů je podpořena více paritními bity. Při zjištění selhání kontroly parity lze informace z vícenásobných paritních bitů použít k obnovení původního datového bitu (Bit-flipping algorithm). 5G NR má jedinečné požadavky na podporu přírustkové redundance prostřednictvím HARQ (Hybrid Automatic Repeat Request), což je mechanismus pro opravu chyb, kdy kombinuje automatickou žádost o opakování přenosu (ARQ) a dopředné opravy chyb (FEC). Přitom je nutné podporovat přizpůsobování rychlostí, aby bylo možné dynamicky přizpůsobovat kódování přiděleným zdrojům. 3GPP standardizovalo QC-LDPC (Quasi-Cyclic LDPC) pro podporu HARQ a přizpůsobení rychlosti.

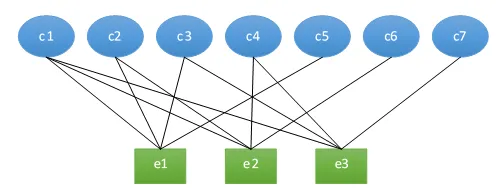
Uvažujme kód založený na paritě, který pracuje s blokem o N bitech. Z N bitů v bloku nese K bitů data a R bitů nese paritu.

N = K + R

Nyní uvažujme kód s délkou bloku 7 bitů a 3 paritními bity na blok.

N = 7, K = 4, R = 3

Tento kód lze považovat za kód s rychlostí 4/7, protože na každých 7 bitů přenosu připadají 4 bity dat.

Pokud je 7 bitů bloku označeno c1 až c7, tak c1, c2, c3, c4 jsou datové bity a c5, c6, c7 jsou paritní bity. Omezení parity můžeme definovat pomocí sčítání ⊕ modulo 2 (exkluzivní OR).

c1 ⊕ c2 ⊕ c3 ⊕ c5 = 0       e1
c1 ⊕ c2 ⊕ c4 ⊕ c6 = 0       e2
c1 ⊕ c3 ⊕ c4 ⊕ c7 = 0       e3

Výše uvedené rovnice lze také znázornit v maticovém tvaru. Každá rovnice odpovídá jednomu řádku matice. Pro sloupce, které v původní rovnici neexistovaly, byly zavedeny členy 0.

c1  c2  c3  c4  c5  c6  c7
1   1   1   0   1   0   0
1   1   0   1   0   1   0
1   0   1   1   0   0   1

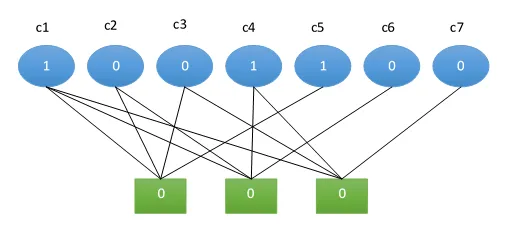
Výše popsané rovnice se obvykle znázorňují, jako Tannerův graf. Datové a paritní bity jsou zobrazeny nahoře. Rovnice, které kladou omezení na datové a paritní bity, jsou znázorněny dole se spojovacími čarami k bitům, na které se vztahují jednotlivá omezení.

• Kódování

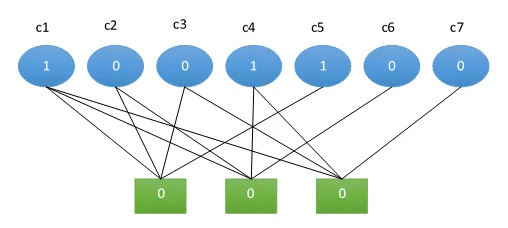
Předpokládejme, že uživatelská data (Data Plane) k odeslání jsou 1001.

c1  c2  c3  c4
1   0   0   1

To aplikujeme na paritní rovnice.

1 ⊕ 0 ⊕ 0 ⊕ c5 = 0
1 ⊕ 0 ⊕ 1 ⊕ c6 = 0
1 ⊕ 0 ⊕ 1 ⊕ c7 = 0

Paritním bitům c5, c6, c7 musí být přiřazeny takové hodnoty, aby byly splněny výše uvedené rovnice. Rovnice budou splněny, pokud bude v každé rovnici nastaven sudý počet bitů.

1 ⊕ 0 ⊕ 0 ⊕ 1 = 0
1 ⊕ 0 ⊕ 1 ⊕ 0 = 0
1 ⊕ 0 ⊕ 1 ⊕ 0 = 0

Výsledkem je následujících 7 bitů.

c1  c2  c3  c4  c5  c6  c7
1   0   0   1   1   0   0

Tannerův graf pro datové bity a uzly omezení je uveden níže.

• Dekódování (Bit-flipping algorithm)

Předpokládejme, že bit c3 je v přijímači (oranžový uzel v horním řádku) přijat chybně. Tato chyba má za následek selhání dvou rovnic kontroly parity (oranžové uzly v dolním řádku).

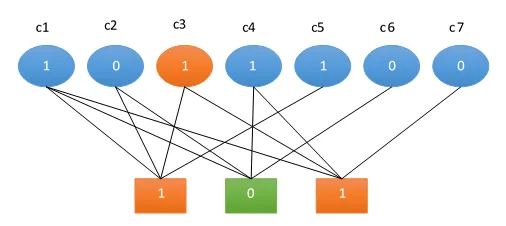
Pokud tedy uzel obdrží více záporných hlasů než kladných, rozhodne se přehodit hodnotu svého výstupního bitu.

Zde bit c3 získává dva záporné hlasy z rovnic kontroly parity. Žádné kladné hlasy nejsou, takže c3 se převrátí. Převrácení bitu vede ke dvěma kladným hlasům pro c3. V tomto okamžiku všechny kontroly parity procházejí, čímž je dekódování dokončeno.

Polární kódy

Polární kódy byly zvoleny stadardizační organizací 3GPP v Release 15. Používají se pouze pro krátké řídící informace (Control Plane), nikoliv pro uživatelská data (Data Plane). Kódovány jsou informace DCI (Downlink Control Information) a UCI (Uplink Control Information) na fyzických kanálech PDCCH (Physical Downlink Control Channel) a PUCCH (Physical Uplink Control Channel). Polární kódy jsou jedinečné tím, že rozdělují kanál na dobré a špatné bitové kanály.

Jak datové kanály polarizovat na extrémně dobré a špatné?

Definujme 2 nezávislé kanály W, které mapují vstupní bity X1, X2 na výstupy Y1, Y2.

Oba kanály implementují transformaci W, která převádí vstup X na výstup Y.

Nyní uvažujme dva vstupy U₁ a U₂, které vstupují do vstupů X₁ a X₂.

X1 = U1 ⊕ U2
X2 = U2

Výsledkem je síť zobrazená níže.

Definujme nyní W, jako binární vymazávací kanál BEC (Binary Erasure Channel), kdy BEC je definován jako:

• X je úspěšně dekódováno do Y (tzn. Y = X) s pravděpodobností:

  1-p
  

• X je neúspěšně dekódován (tzn. Y = ?), v BEC je bit vymazán, takže přijímač je schopen zjistit, že bit byl ztracen s pravděpodobností:

  p
  

Nyní analyzujme síť, o které jsme hovořili výše, z hlediska dvou bitových kanálů (aplikace polarizační transformace):

W⁻ : U₁ → (Y₁, Y₂)
W⁺ : U₂ → (Y₁, Y₂)

W⁻: U₁ → (Y₁, Y₂)

Kanál W⁻ se snaží rekonstruovat vstup přijatý na kanálu U₁. Pokud je kanál W modelován jako BEC, existují následující možnosti:

• Oba kanály jsou úspěšně dekódovány,

    (1-p)²
  

• První kanál je vymazán, ale druhý je úspěšně dekódován,

    p(1-p)
  

• První kanál je úspěšně dekódován, ale druhý kanál je vymazán,

    (1-p)p
  

• Oba kanály jsou vymazány.

    p²
  

Tyto možnosti jsou shrnuty níže:

Zde lze U₁ úspěšně dekódovat pouze v prvním případě, protože U₁ lze extrahovat z U₁ ⊕ U₂, protože U₂ bylo také úspěšně dekódováno. Všechny ostatní případy představují neúspěšné dekódování, protože U₁ nelze extrahovat.

Vytvořili jsme W⁻ s následujícími vlastnostmi:

• U₁ je úspěšně dekódováno,

    (1-p)²
  

• U₁ se nepodaří dekódovat.

    p(1-p) + (1-p)p + p² = 2p-p² = p(2-p)
  

Podařilo se vytvořit horší kanál než BEC. Pokud by BEC měl 30% šanci nebo vymazání:

• Pravděpodobnost úspěchu BEC je 0,7,

• Pravděpodobnost vymazání BEC je 0,3.

Pro bitový kanál W⁻:

• Pravděpodobnost úspěchu W⁻,

    (1,0-0,3)² = 0,7² = 0,49
  

• Pravděpodobnost vymazání W⁻.

    2*0,3-0,3² = 0,6-0,09 = 0,51
  

W⁺: U₂ →(Y₁, Y₂)

Nyní se zaměříme na kanál W⁺. Tento kanál rekonstruuje vstup přijatý na kanálu U₂. U kanálu BEC máme následující možnosti:

• Oba kanály jsou úspěšně dekódovány,

    (1-p)²
  

• První kanál je vymazán, ale druhý je úspěšně dekódován,

    p(1-p)
  

• První kanál je úspěšně dekódován, ale druhý kanál je vymazán,

    (1-p)p
  

• Oba kanály jsou vymazány.

    p²
  

Tyto možnosti jsou shrnuty níže:

Zde lze U₂ úspěšně dekódovat v prvním a druhém případě, protože U₂ bylo úspěšně přijato. Ve třetím případě lze U₂ extrahovat z U₁ ⊕ U₂, protože máme předběžné znalosti o U₁. Poslední případ představuje selhání dekódování, protože není možné extrahovat U₂.

Vytvořili jsme W⁺ s následujícími vlastnostmi:

• U₁ je úspěšně dekódováno,

    (1-p)² + p(1-p) + (1-p)p = 1-p²
  

• U₁ se nepodaří dekódovat.

    p²
  

Podařilo se nám vytvořit lepší kanál než BEC. Pokud by BEC měl 30% šanci nebo vymazání:

• Pravděpodobnost úspěchu BEC je 0,7,

• Pravděpodobnost vymazání BEC je 0,3.

Pro bitový kanál W⁺:

• Pravděpodobnost úspěchu W⁺,

    1,0-0,3² = 1-0,03 = 0,91
  

• Pravděpodobnost vymazání W⁺.

    0,3² = 0,09
  

Výše jsme viděli, že při aplikaci polarizační transformace na BEC s pravděpodobností vymazání p jsme získali dva bitové kanály:

• W⁻ s pravděpodobností vymazání,

    p(2-p)
  

• W⁺ s pravděpodobností vymazání.

    p²
  

Výše uvedené výsledky jasně ukazují, že W⁺ má nižší pravděpodobnost vymazání než W⁻.

0 ≤ p ≤ 1, vyplývá z toho, že p² ≤ p(2-p)

Výsledkem je tedy, že W⁺ je lepší než původní BEC, protože má nižší pravděpodobnost vymazání a lze ho považovate za téměř dokonale spolehlivý a budou do něj umístěny informační bity.

Reference

1. VOKURKA, Lukáš. Proces konverze základnové stanice při přechodu na standard 5G. Ostrava, 2023. Bakalářská práce. Vysoká škola báňská – Technická univerzita Ostrava. Fakulta elektrotechniky a informatiky.

2. MICHALEK, Libor a Roman ŠEBESTA. Mobilní sítě. Ostrava, 2023. Školní skripta. Vysoká škola báňská – Technická univerzita Ostrava. Fakulta elektrotechniky a informatiky.

3. Využívání 5G a jiných sítí elektronických komunikací pro potřeby digitalizace podniků včetně využití moderních informačních systémů. GrantThornton [online]. 2024 [cit. 2024-09-28]. Dostupné z: https://www.mpo.gov.cz/assets/cz/e-komunikace-a-posta/studie-k-narodnimu-planu-obnovy/2024/5/Studie-13.pdf

4. Dynamic Spectrum Sharing: How It Works & Why It Matters. Celona Inc. [online]. 2025 [cit. 2025-03-03]. Dostupné z: https://www.celona.io/5g-lan/dynamic-spectrum-sharing-how-it-works-why-it-matters

5. Samoopravné kódy a limity přenosu zpráv informačním kanálem. Online. Wikisofia. 2013. Dostupné z: https://wikisofia.cz/wiki/Samoopravn%C3%A9_k%C3%B3dy_a_limity_p%C5%99enosu_zpr%C3%A1v_informa%C4%8Dn%C3%ADm_kan%C3%A1lem. [cit. 2025-03-09].

6. 5G NR Channel Codes. Online. TELCOMA. 2025. Dostupné z: https://telcomaglobal.com/p/5g-nr-channel-codes. [cit. 2025-03-09].

7. LDPC — low density parity check code. Online. Medium. 2018. Dostupné z: https://medium.com/5g-nr/ldpc-low-density-parity-check-code-8a4444153934. [cit. 2025-03-09].

8. 5G SA vs 5G NSA vs 5G DSS. TelecomHall FORUM [online]. 2022 [cit. 2025-03-02]. Dostupné z: https://www.telecomhall.net/t/5g-sa-vs-5g-nsa-vs-5g-dss/18225

9. Polar codes. Online. Medium. 2019. Dostupné z: https://medium.com/5g-nr/polar-codes-703336e9f26b. [cit. 2025-03-20].